Werden Objekte von Lichtquellen beleuchtet, so können Bereiche entstehen die unbeleuchtet bleiben. Die werden in zwei Kategorien unterteilt:

Kernschatten Bereich, der von keiner der Lichtquellen beleuchtet wird.
Halbschatten Bereich, der nicht von allen der Lichtquellen (aber mindestens von einer) beleuchtet wird.

Bei punktförmigen Lichtquellen können der Kern- und der Halbschatten klar unterschieden werden. Bei der Verwendung von unterschiedlich farbigen Lichtquellen können farbige Schatten entstehen. Die Farbe der Halbschattens wird von den Quellen bestimmt, die den Halbschatten beleuchten.

Die Aufgaben sind zufällig sortiert. Es stehen Ihnen Tipps und eine Geogebra-Datei zu Verfügung, falls Sie einen Denkanstoß benötigen. Sie können sich auch jeder Zeit an mich wenden. Es steht Ihnen frei die Aufgaben alleine oder in Gruppen zu bearbeiten.

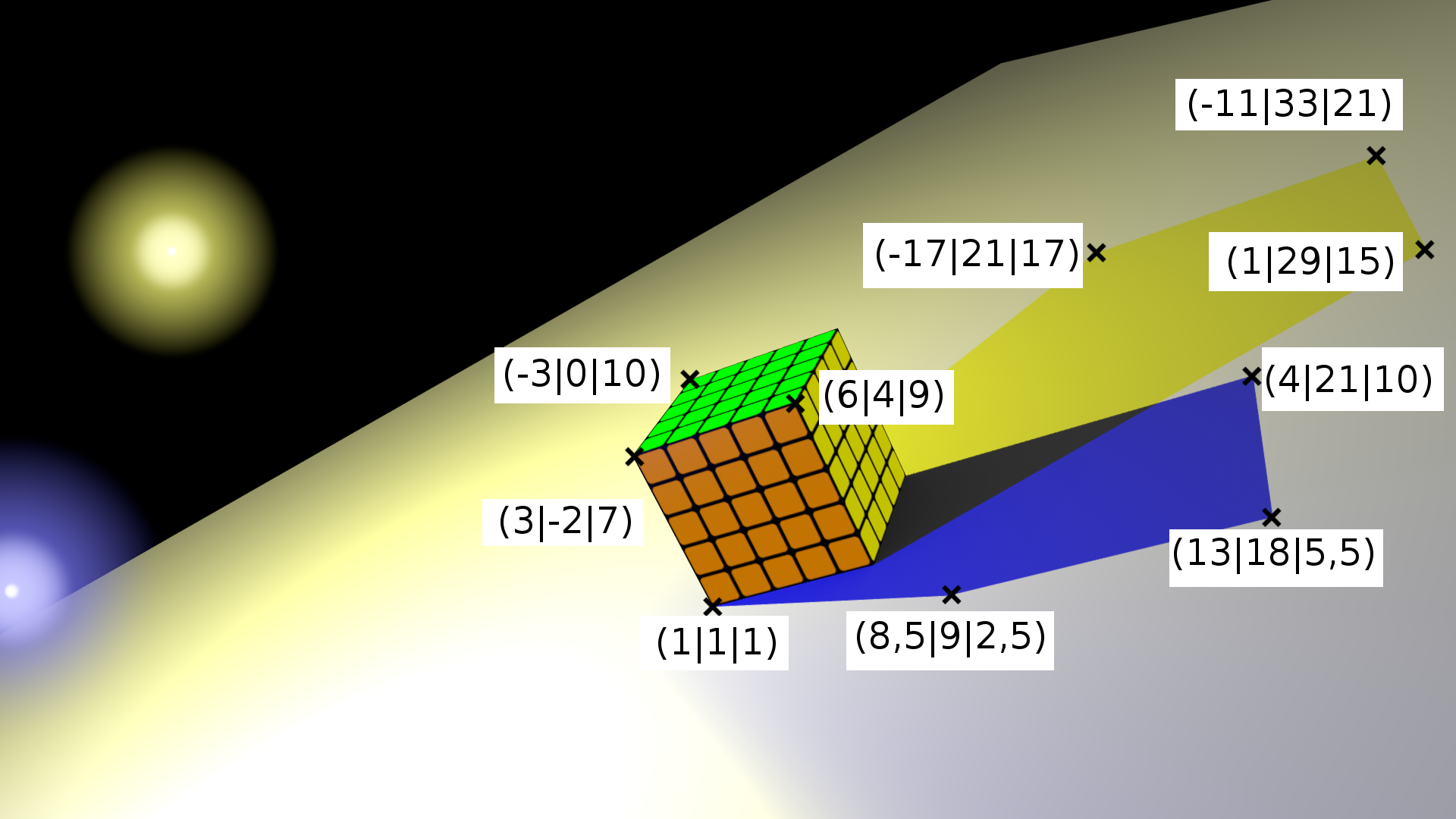
I

Geben Sie die Koordinaten aller Eckpunkte des Würfels an.

II

Bestimmen Sie die Position der jeweiligen Lampen.

III

Bestimmen Sie den Flächeninhalt des Kernschattens, der auf die Platte geworfen wird.

IV

Platzieren Sie die Lampen so, dass der Kernschatten die Form eines gleichschenkligen Dreiecks annimmt.

V

Begründen Sie, dass es sich bei dem Kernschatten, der auf die Platte geworfen wird, um ein rechtwinkliges Dreieck handelt.

VI

Eine Schülerin führt folgende Rechnung durch:

$P_1(1|1|1)$, $P_2(0|6|12)$

\begin{align*} \vec{P_1P_2} &= \begin{pmatrix} 0 - 1 \\ 6 - 1 \\ 12 - 1 \end{pmatrix} = \begin{pmatrix} -1 \\ 5 \\ 11 \end{pmatrix} \\ \vec{OS} &= \vec{OA} + \frac{1}{2} \cdot \vec{P_1P_2} \\ & = \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} + \begin{pmatrix} -0.5 \\ 2.5 \\ 5.5 \end{pmatrix} \\ & = \begin{pmatrix} 0.5 \\ 3.5 \\ 6.5 \end{pmatrix} \end{align*} Formulieren Sie eine Fragestellung im Kontext des \emph{Zauberwürfels}, die durch die obige Rechnung beantwortet werden kann.

VII

Geben Sie eine Parametergleichung eines Lichtstrahles an, der von einer der Lampen ausgestrahlt wird und parallel zu der Platte verläuft, auf der der Zauberwürfel steht.

VIII

Ein Vektor $\vec{n}$, der orthogonal zu einer Ebene $E$ steht, heißt Normalenvektor. Man spricht $\vec{n}$ ist ein Normalenvektor zu $E$.

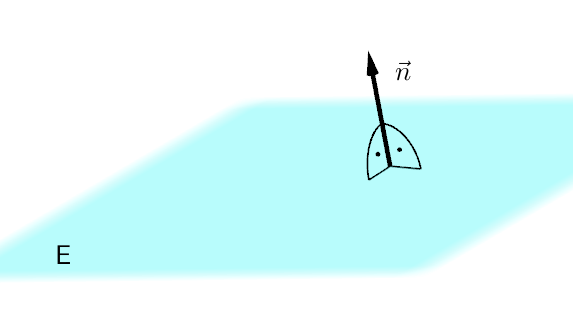
IX

Geben Sie einen Normalenvektor zu der Ebene an, auf der der Zauberwürfel steht. Begründen Sie, dass es sich dabei um einen Normalenvektor handelt. Zusatz: Warum spricht man von einem Normalenvektor und nicht von dem Normalenvektor? Die gelbe und die blaue Lampe werden ausgeschaltet und eine weiße Lampe L3 wird im Punkt~$(3,5|-1|15,5)$ platziert. Es entsteht ein Schatten. Begründen Sie, dass die Eckpunkte des Schattens, der auf die Platte geworfen wird, ein Quadrat bilden.

X

Bestimmen Sie die Winkel des Kernschattens, der auf die Platte geworfen wird.

XI

In die folgende Rechnung haben sich Fehler eingeschlichen. Erklären Sie, wie die Fehler zu Stande gekommen sind.

Zusatz: Korrigieren Sie die Fehler.

XII

Auf die Platte werden zwei Murmeln gelegt und in Bewegung gesetzt. Aufgrund der Reibung auf der Styroporoberfläche bewegen sich die Murmeln mit einem konstanten Tempo und für die Bewegung werden geradlinige Bahnen angenommen. Am Anfang befinden sich die Murmeln in den Punkten $P_1(4|21|10)$ bzw. $P_2(1|29|15)$. Nach einer Sekunde haben die Murmeln die Punkte $R_1(7|13|5)$ bzw. $R_2(-2|23|13)$ erreicht.

XIII

Die Aufgabe ist unnötig kompliziert. Es wäre viel einfacher, wenn wir das Koordinatensystem anders gewählt hätten. Beurteilen Sie diese Aussage.

XIV

Jokeraufgabe - kann öfter verwendet werden. Formulieren Sie eine Fragestellung zu dem gezeigten Kontext und beantworten Sie diese.

Dateien